Global Sensitivity Analysis of the Lotka-Volterra model

The tutorial covers a workflow of using GlobalSensitivity.jl on the Lotka-Volterra differential equation. We showcase how to use multiple GSA methods, analyse their results and leverage Julia's parallelism capabilities to perform Global Sensitivity analysis at scale.

using GlobalSensitivity, QuasiMonteCarlo, OrdinaryDiffEq, Statistics, WGLMakie

function f(du,u,p,t)
  du[1] = p[1]*u[1] - p[2]*u[1]*u[2] #prey
  du[2] = -p[3]*u[2] + p[4]*u[1]*u[2] #predator
end

u0 = [1.0;1.0]
tspan = (0.0,10.0)
p = [1.5,1.0,3.0,1.0]
prob = ODEProblem(f,u0,tspan,p)
t = collect(range(0, stop=10, length=200))


f1 = function (p)
    prob1 = remake(prob;p=p)
    sol = solve(prob1,Tsit5();saveat=t)
    [mean(sol[1,:]), maximum(sol[2,:])]
end

bounds = [[1,5],[1,5],[1,5],[1,5]]

reg_sens = gsa(f1, RegressionGSA(true), bounds)
fig = Figure(resolution = (600, 400))
ax, hm = WGLMakie.heatmap(fig[1,1], reg_sens.partial_correlation, figure = (resolution = (600, 400),), axis = (xticksvisible = false,yticksvisible = false, yticklabelsvisible = false, xticklabelsvisible = false, title = "Partial correlation"))
Colorbar(fig[1, 2], hm)
ax, hm = WGLMakie.heatmap(fig[2,1], reg_sens.standard_regression, figure = (resolution = (600, 400),), axis = (xticksvisible = false,yticksvisible = false, yticklabelsvisible = false, xticklabelsvisible = false, title = "Standard regression"))
Colorbar(fig[2, 2], hm)
fig

using StableRNGs
_rng = StableRNG(1234)
morris_sens = gsa(f1, Morris(), bounds, rng = _rng)
fig = Figure(resolution = (600, 400))
scatter(fig[1,1], [1,2,3,4], morris_sens.means_star[1,:], color = :green, axis = (xticksvisible = false, xticklabelsvisible = false, title = "Prey",))
scatter(fig[1,2], [1,2,3,4], morris_sens.means_star[2,:], color = :red, axis = (xticksvisible = false, xticklabelsvisible = false, title = "Predator",))
fig

sobol_sens = gsa(f1, Sobol(), bounds, N=5000)
efast_sens = gsa(f1, eFAST(), bounds)
fig = Figure(resolution = (600, 400))
barplot(fig[1,1], [1,2,3,4], sobol_sens.S1[1, :], color = :green, axis = (xticksvisible = false, xticklabelsvisible = false, title = "Prey (Sobol)", ylabel = "First order"))
barplot(fig[2,1], [1,2,3,4], sobol_sens.ST[1, :], color = :green, axis = (xticksvisible = false, xticklabelsvisible = false, ylabel = "Total order"))
barplot(fig[1,2], [1,2,3,4], efast_sens.S1[1, :], color = :red, axis = (xticksvisible = false, xticklabelsvisible = false, title = "Prey (eFAST)"))
barplot(fig[2,2], [1,2,3,4], efast_sens.ST[1, :], color = :red, axis = (xticksvisible = false, xticklabelsvisible = false))
fig

fig = Figure(resolution = (600, 400))
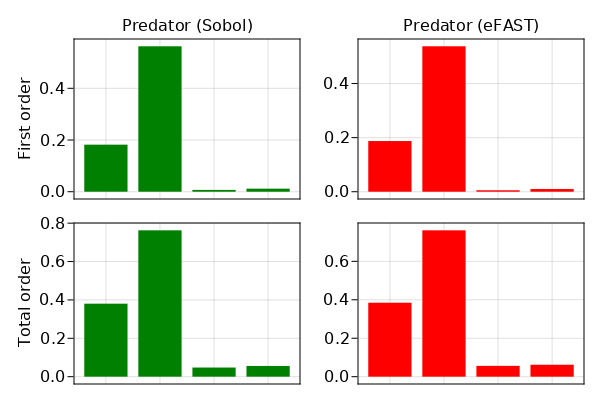
barplot(fig[1,1], [1,2,3,4], sobol_sens.S1[2, :], color = :green, axis = (xticksvisible = false, xticklabelsvisible = false, title = "Predator (Sobol)", ylabel = "First order"))
barplot(fig[2,1], [1,2,3,4], sobol_sens.ST[2, :], color = :green, axis = (xticksvisible = false, xticklabelsvisible = false, ylabel = "Total order"))
barplot(fig[1,2], [1,2,3,4], efast_sens.S1[2, :], color = :red, axis = (xticksvisible = false, xticklabelsvisible = false, title = "Predator (eFAST)"))
barplot(fig[2,2], [1,2,3,4], efast_sens.ST[2, :], color = :red, axis = (xticksvisible = false, xticklabelsvisible = false))
fig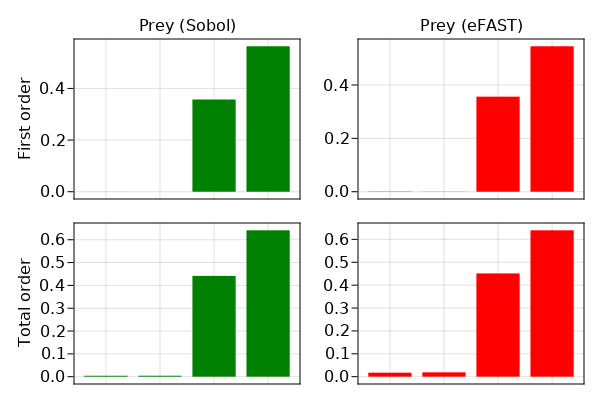

using QuasiMonteCarlo
N = 5000
lb = [1.0, 1.0, 1.0, 1.0]
ub = [5.0, 5.0, 5.0, 5.0]
sampler = SobolSample()
A,B = QuasiMonteCarlo.generate_design_matrices(N,lb,ub,sampler)
sobol_sens_desmat = gsa(f1,Sobol(),A,B)


f_batch = function (p)
  prob_func(prob,i,repeat) = remake(prob;p=p[:,i])
  ensemble_prob = EnsembleProblem(prob,prob_func=prob_func)

  sol = solve(ensemble_prob, Tsit5(), EnsembleThreads(); saveat=t, trajectories=size(p,2))

  # Now sol[i] is the solution for the ith set of parameters
  out = zeros(2,size(p,2))

  for i in 1:size(p,2)
    out[1,i] = mean(sol[i][1,:])
    out[2,i] = maximum(sol[i][2,:])
  end

  out
end

sobol_sens_batch = gsa(f_batch,Sobol(),A,B,batch=true)

@time gsa(f1,Sobol(),A,B)
@time gsa(f_batch,Sobol(),A,B,batch=true)