Solving Kolmogorov Equations with Neural Networks

A Kolmogorov PDE is of the form :

KPDE

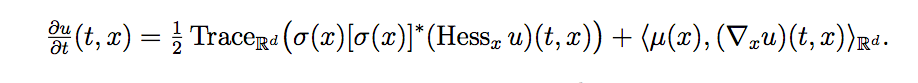
Consider S to be a solution process to the SDE:

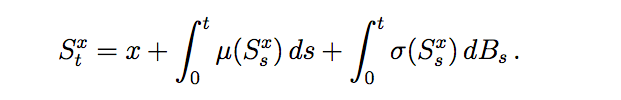
StochasticP

then the solution to the Kolmogorov PDE is given as:

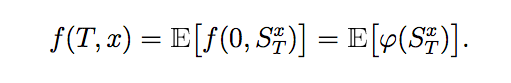
Solution

A Kolmogorov PDE Problem can be defined using a SDEProblem:

SDEProblem(μ,σ,u0,tspan,xspan,d)

Here, u0 is the initial distribution of x. Here, we define u(0,x) as the probability density function of u0.μ and σ are obtained from the SDE for the stochastic process above. d represents the dimensions of x. u0 can be defined using Distributions.jl.

Another way of defining a KolmogorovPDE is to use the KolmogorovPDEProblem.

KolmogorovPDEProblem(μ,σ,phi,tspan,xspan,d)

Here, phi is the initial condition on u(t,x) when t = 0. μ and σ are obtained from the SDE for the stochastic process above. d represents the dimensions of x.

To solve this problem use:

NNKolmogorov(chain, opt , sdealg): Uses a neural network to realize a regression function which is the solution for the linear Kolmogorov Equation.

Here, chain is a Flux.jl chain with a d-dimensional input and a 1-dimensional output.opt is a Flux.jl optimizer. And sdealg is a high-order algorithm to calculate the solution for the SDE, which is used to define the learning data for the problem. Its default value is the classic Euler-Maruyama algorithm.