Detailed Overview of the SciML Software Ecosystem
SciML: Combining High-Performance Scientific Computing and Machine Learning
SciML is not standard machine learning, SciML is the combination of scientific computing techniques with machine learning. Thus the SciML organization is not an organization for machine learning libraries (see FluxML for machine learning in Julia), rather SciML is an organization dedicated to the development of scientific computing tools which work seamlessly in conjunction with next-generation machine learning workflows. This includes:
- High-performance and accurate tools for standard scientific computing modeling and simulation
- Compatibility with differentiable programming and automatic differentiation
- Tools for building complex multiscale models
- Methods for handling inverse problems, model calibration, controls, and Bayesian analysis
- Symbolic modeling tools for generating efficient code for numerical equation solvers
- Methods for automatic discovery of (bio)physical equations
and much more. For an overview of the broad goals of the SciML organization, watch:
Overview of Computational Science in Julia with SciML
Below is a simplification of the user-facing packages for use in scientific computing and SciML workflows.
| Workflow Element | SciML-Supported Julia packages |
|---|---|
| Plotting and Visualization | Plots*, Makie* |
| Sparse matrix | SparseArrays* |
| Interpolation/approximation | DataInterpolations*, ApproxFun* |
| Linear system / least squares | LinearSolve |
| Nonlinear system / rootfinding | NonlinearSolve |
| Polynomial roots | Polynomials* |
| Integration | Integrals |
| Nonlinear Optimization | Optimization |
| Other Optimization (linear, quadratic, convex, etc.) | JuMP* |
| Initial-value problem | DifferentialEquations |
| Boundary-value problem | DifferentialEquations |
| Continuous-Time Markov Chains (Poisson Jumps), Jump Diffusions | JumpProcesses |
| Finite differences | FiniteDifferences*, FiniteDiff* |
| Automatic Differentiation | ForwardDiff*, Enzyme*, DiffEqSensitivity |
| Bayesian Modeling | Turing* |
| Deep Learning | Flux* |
| Acausal Modeling / DAEs | ModelingToolkit |
| Chemical Reaction Networks | Catalyst |
| Symbolic Computing | Symbolics |
| Fast Fourier Transform | FFTW* |
| Partial Differential Equation Discretizations | Associated Julia packages |
| –- | –- |
| Finite Differences | MethodOfLines |
| Discontinuous Galerkin | Trixi* |
| Finite Element | Gridap* |
| Physics-Informed Neural Networks | NeuralPDE |
| Neural Operators | NeuralOperators |
| High Dimensional Deep Learning | HighDimPDE |
* Denotes a non-SciML package that is heavily tested against as part of SciML workflows and has frequent collaboration with the SciML developers.
Domains of SciML
The SciML common interface covers the following domains:
Linear systems (
LinearProblem)- Direct methods for dense and sparse
- Iterative solvers with preconditioning
Nonlinear Systems (
NonlinearProblem)- Systems of nonlinear equations
- Scalar bracketing systems
Integrals (quadrature) (
IntegralProblem)Differential Equations
- Discrete equations (function maps, discrete stochastic (Gillespie/Markov) simulations) (
DiscreteProblemandJumpProblem) - Ordinary differential equations (ODEs) (
ODEProblem) - Split and Partitioned ODEs (Symplectic integrators, IMEX Methods) (
SplitODEProblem) - Stochastic ordinary differential equations (SODEs or SDEs) (
SDEProblem) - Stochastic differential-algebraic equations (SDAEs) (
SDEProblemwith mass matrices) - Random differential equations (RODEs or RDEs) (
RODEProblem) - Differential algebraic equations (DAEs) (
DAEProblemandODEProblemwith mass matrices) - Delay differential equations (DDEs) (
DDEProblem) - Neutral, retarded, and algebraic delay differential equations (NDDEs, RDDEs, and DDAEs)
- Stochastic delay differential equations (SDDEs) (
SDDEProblem) - Experimental support for stochastic neutral, retarded, and algebraic delay differential equations (SNDDEs, SRDDEs, and SDDAEs)
- Mixed discrete and continuous equations (Hybrid Equations, Jump Diffusions) (
DEProblems with callbacks andJumpProblem)
- Discrete equations (function maps, discrete stochastic (Gillespie/Markov) simulations) (
Optimization (
OptimizationProblem)- Nonlinear (constrained) optimization
(Stochastic/Delay/Differential-Algebraic) Partial Differential Equations (
PDESystem)- Finite difference and finite volume methods
- Interfaces to finite element methods
- Physics-Informed Neural Networks (PINNs)
- Integro-Differential Equations
- Fractional Differential Equations
Specialized Forms
- Partial Integro-Differential Equations (PIPDEProblem)
Data-driven modeling
- Discrete-time data-driven dynamical systems (
DiscreteDataDrivenProblem) - Continuous-time data-driven dynamical systems (
ContinuousDataDrivenProblem) - Symbolic regression (
DirectDataDrivenProblem)
- Discrete-time data-driven dynamical systems (
Uncertainty quantification and expected values (
ExpectationProblem)
The SciML common interface also includes ModelingToolkit.jl for defining such systems symbolically, allowing for optimizations like automated generation of parallel code, symbolic simplification, and generation of sparsity patterns.
Inverse Problems, Parameter Estimation, and Structural Identification
Parameter estimation and inverse problems are solved directly on their constituent problem types using tools like SciMLSensitivity.jl. Thus for example, there is no ODEInverseProblem, and instead ODEProblem is used to find the parameters p that solve the inverse problem. Check out the SciMLSensitivity documentation for a discussion on connections to automatic differentiation, optimization, and adjoints.
Common Interface High-Level Overview
The SciML interface is common as the usage of arguments is standardized across all of the problem domains. Underlying high-level ideas include:
- All domains use the same interface of defining a
AbstractSciMLProblemwhich is then solved viasolve(prob,alg;kwargs), wherealgis aAbstractSciMLAlgorithm. The keyword argument namings are standardized across the organization. AbstractSciMLProblems are generally defined by aAbstractSciMLFunctionwhich can define extra details about a model function, such as its analytical Jacobian, its sparsity patterns and so on.- There is an organization-wide method for defining linear and nonlinear solvers used within other solvers, giving maximum control of performance to the user.
- Types used within the packages are defined by the input types. For example, packages attempt to internally use the type of the initial condition as the type for the state within differential equation solvers.
solvecalls should be thread-safe and parallel-safe.init(prob,alg;kwargs)returns an iterator which allows for directly iterating over the solution process- High performance is key. Any performance that is not at the top level is considered a bug and should be reported as such.
- All functions have an in-place and out-of-place form, where the in-place form is made to utilize mutation for high performance on large-scale problems and the out-of-place form is for compatibility with tooling like static arrays and some reverse-mode automatic differentiation systems.
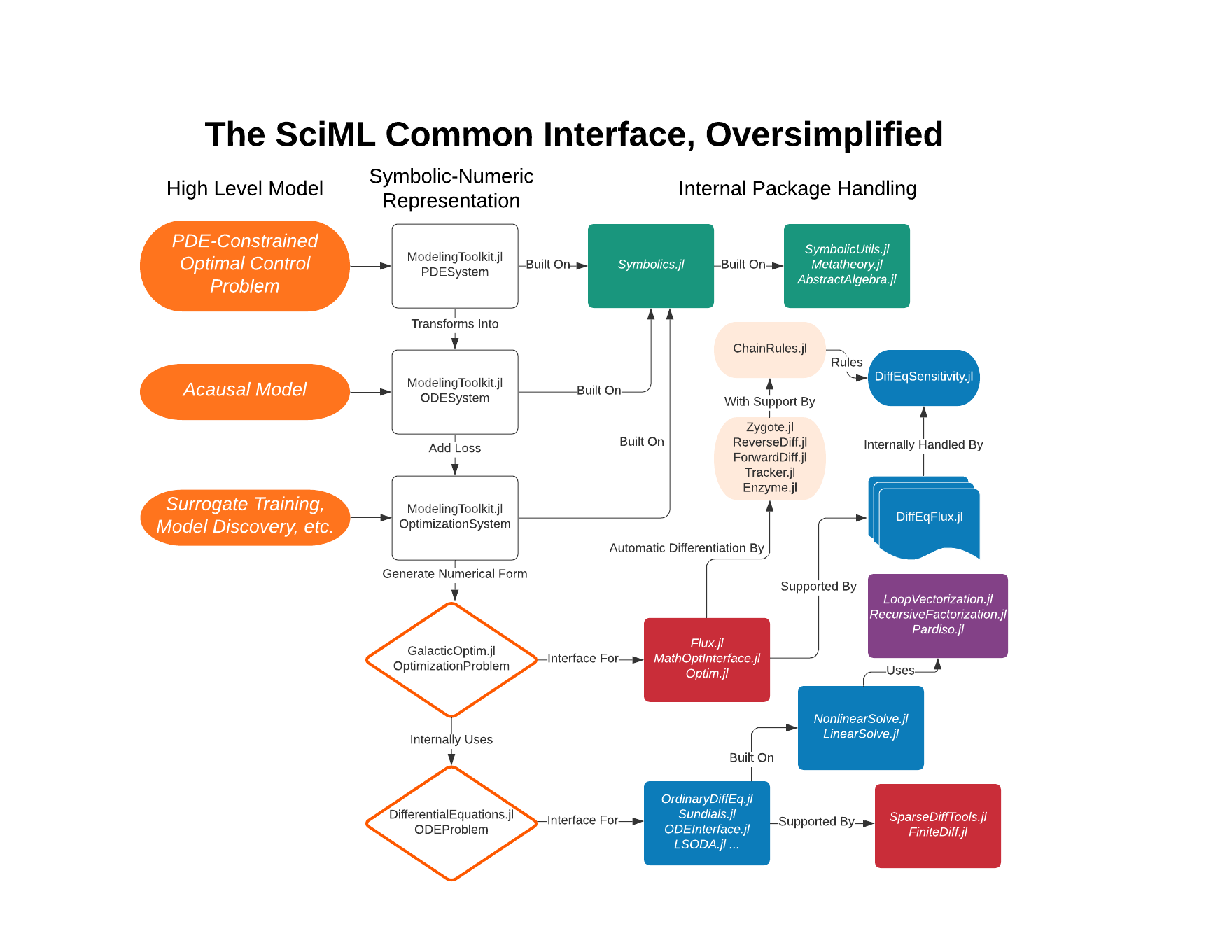
Flowchart Example for PDE-Constrained Optimal Control
The following example showcases how the pieces of the common interface connect to solve a problem that mixes inference, symbolics, and numerics.
External Binding Libraries
- Solving differential equations in R using DifferentialEquations.jl with ModelingToolkit for JIT compilation and GPU-acceleration
- Solving differential equations in Python using DifferentialEquations.jl
Note About Third-Party Libraries
The SciML documentation references and recommends many third-party libraries for improving ones modeling, simulation, and analysis workflow in Julia. Take these as a positive affirmation of the quality of these libraries, as these libraries are commonly tested by SciML developers who are in contact with the development teams of these groups. It also documents the libraries which are commonly chosen by SciML as dependencies. Do not take omissions as negative affirmations against a given library, i.e. a library left off of the list by SciML is not a negative endorsement. Rather, it means that compatibility with SciML is untested, SciML developers may have a personal preference for another choice, or SciML developers may be simply unaware of the library's existence. If one would like to add a third-party library to the SciML documentation, open a pull request with the requested text.
Note that the libraries in this documentation are only those that are meant to be used in the SciML extended universe of modeling, simulation, and analysis and thus there are many high-quality libraries in other domains (machine learning, data science, etc.) which are purposefully not included. For an overview of the Julia package ecosystem, see the JuliaHub Search Engine.